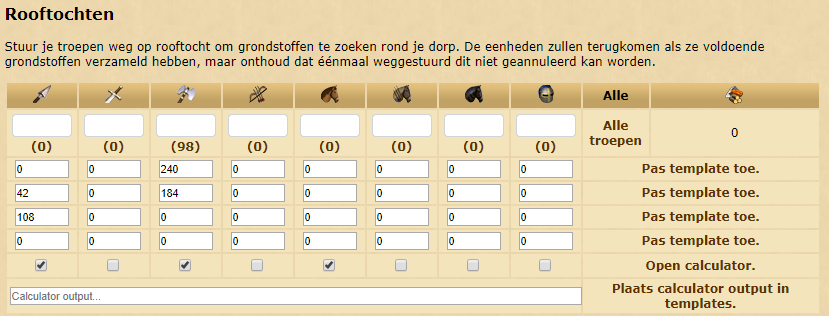
Enter the amount of troops you have.
Check the raids available. (FF, BB, SS or RR. FF is sometimes also known as LR)
Click submit.
The table will show what troop distribution should be used to achieve either the max amount of resources per hour, or the max amount of resources per run.
It’s possible that some troops are left unused, due to rounding. Use those however you like.
Max time away: :
| unit | available | FF | BB | SS | RR |
| spear | 0 | 0 | 0 | 0 | |
| sword | 0 | 0 | 0 | 0 | |
| axe | 0 | 0 | 0 | 0 | |
| archer | 0 | 0 | 0 | 0 | |
| light | 0 | 0 | 0 | 0 | |
| marcher | 0 | 0 | 0 | 0 | |
| heavy | 0 | 0 | 0 | 0 | |
| ideal cap | 0 | 0 | 0 | 0 | |
| res. per run | 0 | 0 | 0 | 0 | 0 |
| res/hour | 0 | 0 | 0 | 0 | 0 |
| hour/run | 0 | 0 | 0 | 0 |
Integration (approved under T13915666)
JSON representation of result:
Iterations to achieve result:
This calculator was approved on tribalwars.nl under ticket number T13900636. The tampermonkey script is as follows:
// ==UserScript==
// @name Scavenge calculator integration
// @namespace https://daniel.dmvandenberg.nl/scripting-tribal-wars/
// @version 0.2.1
// @description try to take over the world!
// @author Daniël van den Berg
// @grant none
// @approved T13915666
// @include https://.tribalwars./game.php?screen=placemode=scavenge*
// @require https://gitweb.dmvandenberg.nl/snippets/TWAjax.user.js?p=tribalwarsscripts.git;hb=master;a=blob_plain;f=snippets/TWAjax.user.js
// @require https://gitweb.dmvandenberg.nl/snippets/PersistentInput.user.js?p=tribalwarsscripts.git;hb=master;a=blob_plain;f=snippets/PersistentInput.user.js
// @require https://gitweb.dmvandenberg.nl/snippets/Retrieve%20units.user.js?p=tribalwarsscripts.git;hb=master;a=blob_plain;f=snippets/Retrieve%20units.user.js
// @updateURL https://gitweb.dmvandenberg.nl/Scavenge%20calculator%20integration.user.js?p=tribalwarsscripts.git;hb=master;a=blob_plain;f=Scavenge%20calculator%20integration.user.js
// @downloadURL https://gitweb.dmvandenberg.nl/Scavenge%20calculator%20integration.user.js?p=tribalwarsscripts.git;hb=master;a=blob_plain;f=Scavenge%20calculator%20integration.user.js
// ==/UserScript==
(async function() {
'use strict';
let sUniquePrefix = "e08ed5e5-559a-4138-b37f-c135697a2565_";
let oUnits = await window.doRetrieveUnits();
window.oUnits = oUnits;
let tTableSquad = document.querySelector("#scavenge_screen table.candidate-squad-widget tbody");
if (!tTableSquad){
return;
}
let rRow = document.createElement("tr");
tTableSquad.appendChild(rRow);
let aUnits = Array.from(document.querySelectorAll(".unit_link")).map((e)=>{return e.getAttribute("data-unit");});
for (let sUnit of aUnits){
let eCol = document.createElement("td");
rRow.appendChild(eCol);
let chkCheckbox = document.createElement("input");
eCol.appendChild(chkCheckbox);
chkCheckbox.setAttribute("type","checkbox");
chkCheckbox.id = `${sUniquePrefix}${sUnit}`;
window.doMakePersistentInput(chkCheckbox);
}
let eColSendToCalculator = document.createElement("td");
eColSendToCalculator.colSpan = 2;
rRow.appendChild(eColSendToCalculator);
let aSendToCalculator = document.createElement("a");
eColSendToCalculator.appendChild(aSendToCalculator);
aSendToCalculator.innerText = "Open calculator.";
if (!window.game_get_config){
window.get_game_config = await window.$.twAjax("/interface.php?func=get_config");
}
aSendToCalculator.addEventListener("click",()=>{
let aCheckedUnits = aUnits.filter((sUnit)=>{
return document.getElementById(`${sUniquePrefix}${sUnit}`).checked;
});
let oCheckedUnits = aCheckedUnits.reduce((oRet, sUnit)=>{
oRet[sUnit] = oUnits[sUnit];
return oRet;
}, {});
let oParams = oCheckedUnits;
oParams.iWorldSpeed = window.get_game_config.querySelector("config speed").innerHTML * 1;
oParams.iUnlocked = 4 - document.querySelectorAll(".scavenge-option .lock").length;
let sURL = `https://daniel.dmvandenberg.nl/scripting-tribal-wars/tribal-wars-scavenge-calculator/?${new URLSearchParams(oParams).toString()}`;
window.open(sURL,'popup','width=600,height=600');
return false;
});
let eRowToTemplate = document.createElement("tr");
tTableSquad.appendChild(eRowToTemplate);
let eColTemplateInput = document.createElement("td");
eRowToTemplate.appendChild(eColTemplateInput);
eColTemplateInput.colSpan = aUnits.length;
let eTemplateInput = document.createElement("input");
eColTemplateInput.appendChild(eTemplateInput);
eTemplateInput.style="width:100%;";
eTemplateInput.placeholder="Calculator output..."
let eColToTemplate = document.createElement("td");
eColToTemplate.colSpan = 2;
eRowToTemplate.appendChild(eColToTemplate);
let eToTemplate = document.createElement("a");
eToTemplate.innerText="Plaats calculator output in templates.";
eColToTemplate.appendChild(eToTemplate);
eToTemplate.addEventListener("click", ()=>{
if (document.getElementById("scavenge-0") == undefined){
alert("Please install scavenge templates. See https://daniel.dmvandenberg.nl/scripting-tribal-wars/small-scripts/");
return;
}
let oInput = JSON.parse(eTemplateInput.value);
if (!oInput){
return;
}
let fnScavenge = (eRow, oScavenge)=>{
aUnits.forEach((sUnit, iUnitIndex)=>{
let eInput = eRow.children[iUnitIndex].firstChild;
eInput.value = oScavenge[sUnit];
let event = new Event('change');
eInput.dispatchEvent(event)
});
};
fnScavenge(document.getElementById("scavenge-0"), oInput.FF);
fnScavenge(document.getElementById("scavenge-1"), oInput.BB);
fnScavenge(document.getElementById("scavenge-2"), oInput.SS);
fnScavenge(document.getElementById("scavenge-3"), oInput.RR);
});
})();If your world(speed) is not here:
Please leave a comment below. In order for me to add a world, I need the following information:
– The name of the world (start of the URL).
– The game speed of the given world.
How this works
In the game javascript the following formula can be found for how much a scavenge brings in:
iCap * iRatiowhere iCap is the total capacity of all units, and iRatio is 10% for the first hunt, 25% for the second, 50% for the third and 75% for the fourth.
The following equation is found for the duration of a scavenge:
((Math.pow(Math.pow(iCap, 2) * 100 * Math.pow(iRatio, 2), 0.45) + 1800) * df)In this formula, df stands for the duration factor. This seems to be loosely based on the world speed. On NL73 it’s 0.9045869428, on NLP9 it’s exactly 1. By throwing the data of the duration_factor and game_speed into google sheets and letting sheets calculate a power trendline, I found that the formula is game_speed^(-0.55).
| World | duration_factor | game_speed | unit_speed |
| zz1 | 0.8845033719 | 1.25 | 0.8 |
| nlp9 | 1 | 1 | 1 |
| nl71 | 0.6830201284 | 2 | 0.5 |
| nl72 | 1 | 1 | 1 |
| nl73 | 0.9045869428 | 1.2 | 0.8 |
This gives the following formula for resources per hour:
iCap * iRatio / ((Math.pow(Math.pow(iCap, 2) * 100 * Math.pow(iRatio, 2), 0.45) + 1800) * df)This function can be summed four times, with a spread of the iCap (or capacity) for all different ratios. Let’s assume “a” to be an array representing the spread of carry capacity over the four scavenges, where the sum of the 4 elements <= 1. This gives the following:
iCap * a[0] * 0.10 / ((Math.pow(Math.pow(iCap * a[0], 2) * 100 * Math.pow(a[0], 2), 0.45) + 1800) * df) +
iCap * a[1] * 0.25 / ((Math.pow(Math.pow(iCap * a[1], 2) * 100 * Math.pow(a[1], 2), 0.45) + 1800) * df) +
iCap * a[2] * 0.50 / ((Math.pow(Math.pow(iCap * a[2], 2) * 100 * Math.pow(a[2], 2), 0.45) + 1800) * df) +
iCap * a[3] * 0.75 / ((Math.pow(Math.pow(iCap * a[3], 2) * 100 * Math.pow(a[3], 2), 0.45) + 1800) * df)Now this is a formula that we could start brute-forcing to find the ideal “a”. Once we find that one, we can simply multiply the total capacity by the individual elements of “a” in order to find how much capacity we should send on a given scavenge hunt.
With this initial “a” we calculate how much we’d get per hour, and save this in a variable. After that, we move half of a[0] to a[1]. We also do the opposite. Of those three options, we check which gives the highest revenue and keep that one.
Given that all scavenges are enabled, we'd start with [0.25,0.25,0.25,0.25]. Our second attempt would be [0.125,0.375,0.25,0.25], and our third attempt would be [0.375,0.125,0.25,0.25].
Next up, we do the same, but then with a[1] and a[2]. After that, we do it with a[2] and a[3]. And then we start over.
We keep doing this, until our total revenue does not increase any more. At that point “a” is distributed so that it gives us the ratio of carry capacity required to get the maximum amount of resources per hour. We then calculate that back to how many troops are required to get as close to that required carry capacity, and show this as an output.

Goedemiddag Daniel,
Je rooftochten script ziet er goed uit, de calculatietool heeft me al veel vooruit geholpen. Nu is het echter zo dat wanneer ik het script probeer te installeren door de ‘Download Integration’ button te gebruiken, ik een foutmelding krijg;
”Deze site is niet bereikbaar
https://gitweb.dmvandenberg.nl/Scavenge%20calculator%20integration.user.js?p=tribalwarsscripts.git;a=blob_plain;f=Scavenge%20calculator%20integration.user.js;hb=master#bypass=true werkt even niet, of de pagina kan verhuisd zijn naar een nieuw webadres.”
Ben nog een beetje nieuw met zo’n soort scripts, maar weet jij of dit verholpen kan worden?
Alvast bedankt!
Met vriendelijke groet,
Rob
Goedemorgen Rob,
Dank je voor je bericht. Ik had toevallig gisterochtend wat serveronderhoud uitgevoerd, en blijkbaar waren mijn scripts daarmee even tijdelijk niet bereikbaar. Ik heb dit zojuist opgelost, je kan het script nu weer downloaden!
Wow Great calculator thank you!
When I install the script however, I click “Open Calculator” And nothing happens. What am I doing wrong?
Thank you so much!
Hi Gavin,
On what server are you playing? I’m guessing it’s a bug with specific troops being enabled/disabled.
Edit:
I have just placed an update that should make the script more robust. Can you try updating it, and then try again?
Thank you very much!
Thanks for keeping this tool up to date Daniël helps us alot out there with scavenging <3
I have seen in the scripts section other scripts is there a way to get an english description for it or is it only in netherland?
Thanks in advance!
Hi Christian,
I have not provided English translations for any scripts, as I’ve been told that no servers but the .nl servers allow the use of userscripts. If you could provide me with information that proves otherwise, I’d definitely be interested to start working on translated versions!
Hi, I managed to confuse it by setting a maximum away time which was too short for the number of troops I was using. It reported in the table the time I specified, but used troops that took far longer.
Is it worth setting this up so that it’s aware and holds troops back to meet the max time restriction?
Hey Darren,
Thank you for reporting this! To be honest I thought I fixed this a long time ago… But this time it should really be fixed 😉
Hi, I love your tool but I think there is something wrong with the code (or I am using it wrong).
If you use the option most resources per hour on a large army the run times don’t come close to the one in game (even when you would have selected a wrong world speed) and the gathered resources are to low as well.
In addition under “Make all scavenges take equally long” the shown run time isn’t close to etch other.
Hope you are having a nice weekend and have a nice day
Hi Stephan,
Can you try it again? I think I fixed it.
Hello,
when I download script, to using him I must have premium account od tribal wars?
I am asking because I dont see any choice to calculate.
Thanks
Hi Martin,
On what world (what URL) do you play? Can you verify that the script is active on the scavenge screen? The script is currently only active on any domain containing “.tribalwars.”. If it is, please let me know, I’ll mail you with some more questions (with screenshots).
Hallo Daniël,
Wat ziet het er mooi uit!
Heb het al handmatig al gebruikt maar wil heel graag het script downloaden voor w75 en w76
Heb je die ook kan en klaar zeg maar?
Ik ben niet handig in zelf dingen veranderen in scripts namelijk 😀
Hoor graag van je…
Lizz
Hoi Lizz,
W75 lijkt op snelheid 1.00 te draaien, W76 op snelheid 2.00. Ik heb ze toegevoegd in het selectieveld ?
Hallo,
Echt een top script man ! Bedankt!
Alleen gebruik hem nu dan op de nieuwe wereld en ging paar dagen goed en hij werkt nog wel hoor alleen wat er nu gebeurt is vreemd
Open calculator en Templates ding moet ik een heel stuk naar rechts gaan op de pagina.
en je kan ook toch de troepen selecteren met die vinkjes. er staat een hele rij met vinkjes die er niet hoeven staan enz..
Weet jij hoe dit komt? want het maakt het namelijk beetje onoverzichtelijk plus is irritant haha.
Groetjes Stefan
Hoi Stefan,
Nee, geen idee eigenlijk. Kan je eens al je andere scripts uitschakelen en kijken of het dan nog steeds gebeurt? Bij mij werkt het namelijk nog steeds gewoon goed, dus dit klinkt voor mij alsof er een ander script in de weg zit.
Nice one on the above.
Another request though please?
Could you add UK World 52?
Game speed – 1.8
Unit speed – 0.625
2nded please 🙂
Also spotted another slight bug, it’s allowing <10 troop scavs to be suggested with low numbers of troops (example 76sp, 65sw on first three levels)
I’ve added UK52. I know about the <10 troops scavenging "bug", but to be honest, it's not worth fixing. The amount of resources gained is minimal, and the technical complications are quite big. The system would have to make multiple passes to calculate the best outcome. Say it thinks 5 should go to the first scavenge and 15 to the second, is it then more efficient to send out 0 and 20 or 10 and 10? So thanks for mentioning it, but yeah, not really worth fixing to me.
Hi, excellent Calculator!!
I am receiving an error when trying to download the script, is this a problem on my end?
Regards,
Richard
Thanks for mentioning it, it’s back online now!
Hello,
Excellent calculator!!
I am having trouble downloading the script:
This site can’t be reachedThe web page at https://gitweb.dmvandenberg.nl/Scavenge%20calculator%20integration.user.js?p=tribalwarsscripts.git;a=blob_plain;f=Scavenge%20calculator%20integration.user.js;hb=master might be temporarily down or it may have moved permanently to a new web address.
Is this a problem on my end??
Kind regards,
Richard
Thanks for mentioning it, it’s back online now!
The integration link is broken.
Thanks for mentioning it, it’s back online now!
Hi, optimise for resources per run, with an 8hr limit and largish troops isn’t working for me. Its not using all troops, the first level isn’t being utilitised at all, and the second tier is only around 3hrs long.
Sorry to keep reporting this stuff.
Don’t be sorry, thank you so much for mentioning it! I’ve gone through all the code again, and fished out a couple inconsistencies and problems. So, it’s fixed! (Or at least, as good as. It still leaves 300 troops behind but if I’d make it fix that it would take too long to calculate, and it’s only 3% of the troops on the slowest run, so probably <1% resource gain.)
Hey,
would it be possible that you request whitelisting you Script for the German version of this game? https://www.die-staemme.de/
This would be very nice.
Thank you and kind regards,
Lucas
http://forum.die-staemme.de/index.php?threads/160346/
Hi Lucas,
My German is absolutely terrible, but you’re free to request whitelisting yourself. If you get some sort of number (like a ticket number or so) that I can display to show others it’s whitelisted, I’ll happily add it to this page.
If the author needs to make the request, you can mention that I asked you to request it on my behalf.
With kind regards, Daniël
Awesome, thanks so mucj for taking the time to di this, it’s just amazing
Hi,
Thank you for this great calculator! That’s exactly what I was looking for.
Could you add the German world?
w184
Game speed 1.25
Or is that the same setting as world ZZ1 in the calculator?
greetings
Hi Max,
It’s indeed the same as ZZ1, I added it to the form though 😉
Hey Daniel,
First off thank you for this script it has been a huge help in maximizing my scavenging profits! I was wondering if this script has been approved on any worlds other then the nl world? I am currently playing w53 on UK but didn’t want to use the script incase it wasn’t approved.
Thanks in advance!
Hi Jason,
As I do not have an account on any server but the Dutch servers, I can’t make any support tickets relating those worlds. As far as I’m aware scripts like these are never blocked, but if you want to be sure, you can always contact support.
If you do and they verify that it’s okay, please let me know the ticket number, I’ll add that to the page so your fellow UK players know it’s approved!
With kind regards, Daniël
Hello,
is there some way how to apply this calculator for a czech tribal war server? I have tried it for czech S74 server (server speed 1.2), however the time for a singe run with equal troops is still different than the one which is given by the calculator. I would love to use it for the new s75 server which will have speed 1.0.
Thank you very much and have a nice day.
Hi Robert,
It should just work… Can you give me an example with numbers? How many troops are you putting in, what’s the duration in game?
Yes, of course. For instance, when I try to send:
1) 100 spears for the 1st level
resources: 83, 83, 84
time: 0:49:03
2) 100 spears for the 2nd level
resources: 208, 208, 209
time: 1:13:28
Could we have the speed for the new UK world please?
Game = 1.5
Unit = 0.625
Hi Darren,
I added speed 1.5!
The results are coming out well off in terms of res/run and res/hour.
I’m getting about 1/3 of what it thinks. Have you got the speeds right?
I’m an idiot. You total all three res types. Ignore me pls ?
Hello,
Thank you a lot for your work, it’s really helpful efficient and easy to use !
Could you add the world 66 ?
Worldspeed : 1.4
(I don’t know if it is of any help but here is world’s settings page’s url : https://fr66.guerretribale.fr/page/settings)
Have a good day !
Hi Adrien,
I added the world speed!
Daniël
Hi,
Is it possible run this script on divokekmeny.cz?
Thanks
Hi Milan,
If you change the //match line it should work. No guarantees though!
Daniél
Hi, it’s a great tool, thank you!
Are these the equivalent of the UK scavenges?
On UK server they are called:
Lackadaisical Looters – Level 1
Humble Haulers – Level 2
Clever Collectors – Level 3
Great Gatherers – Level 4
Can I assume that FF = level 1
BB = level 2
SS = level 3
RR = level 4?
Thanks
Hi Jack,
Those should be identical. You can of course check the reources per run to make sure, those should be quite close.
Thank you!
Are there any English versions of your scripts available at the moment?
what does the ideal cap mean?
Hi Titus,
Ideal cap stands for the distribution of carrying capacity required to retrieve the optimal amount of resources.
Hello mate,
Great work on the calculator. I was wondering if you could help me on integrating it into my TW account. Any other script i have used i just copy a line of JS into the “Target-URL” box. When i click download on your file i get an actual JS file that im unsure of what to do with.
Could you help me out with integrating this please?
Regards,
Jack
Hi Jack,
For this type of scripts you need to install the chrome extension “tamper monkey”.
Daniël
Hi Daniel,
Im having issues in the portuguese server.
The “Open calculator” is fine!
But the “Plaats calculator output in templates” is alerting me that im missing the small-script, im sending you a print of my problem.
https://prnt.sc/10lgfcm
I already visited the url, and installed, but the problem persist.
Thank you!
Hi Edd,
An update to tribal wars had caused this script (the scavenge templates) not to work any more. Once updated, it should work again.
Daniël
I found a strange bug. If i calculate 1000 speers for max res per hour i get around 3460 Ress/hour
and the longest time away is 3:48
If i set a maximum time away on 4 hours i would expect the same result.
But now we have 3050 Ress/hours and max time away 4 hours?
Hi Florian,
As this script attempts to brute force the best solution, it’s entirely possible that it doesn’t always end up at the most optimal solution. Without rewriting the entire code, unfortunately there’s not a lot I can do about this.
Dear Daniel,
At first thank u for ur amazing tool that u created to make all our tribal wars life’s an easier life for so many years ❤️
I’m using ur calculator for quite a while now and never had problems.
Now out of nowhere the estimated times the calculator shows me do not match the numbers in the game.
I’m actively playing on CAS14DE which is at world speed 1 which i can choose with ur calculator but only the last 3 days it gives me numbers that are about an hour ten longer in the game then the estimation here.
Maybe u can help me out here ?
Best wishes and stay healthy
Julian
NVM!!!
Don’t bother found the problem 🙂
Delete pls
us56
speed: 1.6
us53*
also, thanks for all your work, it’s truly awesome! i’ve read some of the above messages, and i installed tampermonkey on chrome. when i go to install the script, am i just supposed to copy the entire downloadable js scripts and paste it into the “Target URL” box? because that doesn’t seem to be working. it just says “this site can’t be reached”. thanks.
Hi Celestium,
I added the world speed!

With tampermonkey installed, when you click the “Download Integration” button you should get a screen from tampermonkey.
I did update my server lately, can you try again?
If that doesn’t work, you can also create a new script in tampermonkey and paste the script in there.
Awesome, thanks. The new world speed seems to work pretty well. And, i now have new options on my scavenge page: “Open calculator.”, and “Plaats calculator output in templates.”. However, when i put the “JSON representation of result” into the text field, and click the “Plaats calculator output in templates.”, chrome gives me a little window at the top that says:
“us53.tribalwars.us says
Please install scavenge templates. See https://daniel.dmvandenberg.nl/scripting-tribal-wars/small-scripts/”
I’ve visited that page, and installed the template integration in tampermonkey using the “Install” button. that didn’t seem to work, still got the same message. i then copies the script and pasted it as a new script in tampermonkey, saved it, then deleted the original. same thing. doesn’t seem to work for me.
Looking at the other posts, it may be an update issue?
kan hem niet downloaden… link werkt niet
Het script is nu te kopieren/plakken.
Hey man, is the intergation working?
I put the script in here, there’s a simple copy button now. Due to security issues in modern browsers auto-adding is not allowed any more, so you’ll have to manually copy/paste it into tampermonkey. The integration should be working still, but as I don’t play myself any more I’m not sure.
can’t download
I put the script in here, there’s a simple copy button now. Due to security issues in modern browsers auto-adding is not allowed any more, so you’ll have to manually copy/paste it into tampermonkey.